美國最受歡迎的數學教授、
《數學教你不犯錯》作者喬丹.艾倫伯格的最新大作,
以數學對現實世界進行深度的解析。
本書帶你邂逅新的幾何學:
流行病傳播的幾何學、混亂美國政治進程的幾何學、
職業棋士的幾何學、人工智能的幾何學、
英語的幾何學、財金的幾何學、物理的幾何學,
以及詩的幾何學。
「這本書怎麼可能這麼有娛樂性?這不合理啊!它揭示了幾何思維如何促成從更公平的美國選舉、到更好的流行病規劃。」―紐約時報
幾何學不是歐幾里得,早就不是了。它不是散發著教室氣息的文化遺產,而是一門活生生的學科,正以前所未有的速度前進。
這本書讓你邂逅新的幾何學。
包括我們正在經歷的COVID-19流行病的傳播。本書告訴你流行病傳播不是醫學,而是數學,更嚴格來說是幾何學。因此,該如何透過找出流行病的圖形,來理解每日染疫人數的變化,預估疫情高峰與結束的時間,並說明為什麼流行病的控制不追求完美主義?
還有美國式民主的政治進程,若不是運用幾何學的洞察,還真的不容易揪出背後的操作與不公平!作者舉他的故鄉威斯康辛州為例,說明共和黨人如何透過選區劃分,讓共和黨在國會中的席位屹立不搖,以此介紹了「傑利蠑螈」的存在。以及若沒有幾何學的抽絲剝繭,分辨其中政治操作的訣竅,還真容易遭到蒙蔽。果然只要改變選區的形狀,就能改變選舉結果!
作者更一一分析職業棋士的幾何學、人工智能的幾何學、英語的幾何學、財金的幾何學、物理的幾何學,以及詩的幾何學。原來,每個事物都有其幾何結構,數學不只是理性的分析和掌握,更是對於事物內在形狀的直覺感知和洞悉,幾何學可說是數學中最饒富興味、最感性的一支!
…
本書為《紐約時報》暢銷書《數學教你不犯錯》作者喬丹.艾倫伯格的新作,艾倫柏格本身為世界一流的幾何學家,在本書中顛覆我們對幾何的認知,開啟我們對幾何的嶄新力量的大門,讓我們對幾乎所有事物產生更深入的理解與認識。
過去兩百年間在教室裡的典型幾何學課程,是將歐幾里得當成博物館文物,那些證明是用來記憶、背誦、甚至欣賞的,一個人如何能想出這些證明完全沒被提及。但如今我們不再要求學生背誦歐幾里得,而是透過幾何學訓練學生養成嚴謹推理的心智習慣。但幾何學的意義遠遠超過這個。
但凡科學、政治以及哲學問題背後都隱藏著幾何結構。在希臘文中,「幾何學」這幾個字具有「測量世界」的偉大含意,但這層意義低估了幾何學。事實上,幾何學不僅能測量世界,還能闡明世界。幾何學會問:物體的位置和樣貌如何?哪些事物彼此相近?你可以如何從一件事推出另一件事?這些都是重要的問題。
透過幾何學的眼鏡,不難發現以下問題都與幾何學息息相關:
•民主政治該如何選擇代表?
•該如何阻止傳染病席捲全球?
•電腦如何學習下棋?
•為什麼對電腦來說,學會下棋比學會閱讀要簡單多了?
•古希臘的黃金比例可以用來預測股市嗎?
•如果你的孩子想學會思考,該在學校裡學習什麼?
此時此刻,幾何學正在隨著人工智能,深入到我們生活的每一個面向,重新塑造我們居住的城市成為新興的幾何學都市。且讓我們穿透表面現象,看穿事物內在形狀,從而瞭解事物背後的運作。
出奇有趣的新書……《形狀》真的把幾何學變有趣了……以艾倫伯格的妙語如珠(以及他對19世紀美髯的欣賞),《形狀》的真功夫在於將幾何井井有條地化為文字。……對艾倫伯格來說,幾何不是逃離現實的去處,而是生命中的一股力量——可以用來為善或為惡,也可以用來玩味。幾何連結擴展了我們對世界的看法,以及真實與抽象之網。如同詩人瑞塔‧多芙所寫:「我證明了一個定理,然後房子變大了」。
—Parul Sehgal, The New York Times
艾倫伯格的詳盡闡述,對數學中人性的探索,以及令人拍案叫絕的最終章,捍衛以公平及科學為基礎的民主,再再提醒我們,為何他是美國最受歡迎的數學教授。
—Daily Beast
引人入勝、鞭辟入裡。
—The New York Times Book Review
艾倫伯格從幾何的意義寫到幾何在現代社會中的作用,層面廣泛,眼界益發廣闊,文筆益發活潑。
—The Telegraph
[喬丹‧艾倫伯格]維持了與前作一貫的魅力……幾乎人人都會喜愛艾倫伯格的文章和見識。
—Harvard Magazine
將嚴謹的數學寫得深入淺出、妙趣橫生……一則則幽默的數學軼聞,引人深入數學理論之海。
—Kirkus
數學教授艾倫伯格(《數學教你不犯錯》)以輕快的筆觸,呈現深度數學對現實世界問題的解析……對數學感興趣的讀者對世界將有更深刻的瞭解。
—Publishers Weekly
《形狀》是數學著述中的得意之作,以流暢文筆及令人捧腹的幽默揭露深刻的真理——從距離的性質到隨機的可預測性——以及深刻的錯誤——從歷史的錯誤歸功到最高法院大法官的冥頑不靈。艾倫伯格對其主題及讀者的熱情洋溢筆端,使我們深感幸運,得以聽他以親切口吻娓娓道來他最喜愛的主題,數學。
—Cathy O’Neil, author of Weapons of Math
作者∣喬丹.艾倫伯格 Jordan Ellenberg
威斯康辛大學麥迪遜分校(University of Wisconsin-Madison)數學系的維拉斯傑出成就教授(Vilas Distinguished Achievement Professor)。《紐約時報》暢銷書《數學教你不犯錯》作者。
譯者∣蔡丹婷
師大翻譯研究所畢業。坐過辦公室,當過英文老師,但還是最喜歡翻譯,最愛的是家人。極喜歡窩在家中推敲字句的日子,更喜歡透過不同語言接觸新知,夢想是能使用八國語言。過去二十年主要為HBO頻道及Discovery系列頻道翻譯字幕,譯有《綠手指聖經》。
推 薦 很難明白這其實很簡單 洪萬生
前 言 物體的位置及其樣貌
第01章 「我投歐幾里得一票」
第02章 一根吸管有幾個洞?
第03章 不同事物、相同名字
第04章 人面獅身像的碎片
第05章 「他的風格是無敵」
第06章 試誤的神祕力量
第07章 人工智能登山學
第08章 你是你自己的負一層表親及其他地圖
第09章 三年的星期日
第10章 今天發生的事明天也會發生
第11章 可怕的增長率
第12章 葉中之煙
第13章 空間的皺摺
第14章 數學如何破壞民主(又如何加以挽救)
結 語 我證明了一個定理 然後房子擴大了
誌謝
注釋
圖片來源
【專文推薦】
◎洪萬生 (台灣數學史學會理事長)
「本書有關美國選舉制度及疫病(特別是 COVID-19)的數學問題(本書歸類為幾何學)之說明,一定可以讓關注或參與類似活動的博雅君子感同身受。中學教師也可以在課堂上引進這些例子及其說明,來強調數學並非遠在天邊的彩虹,而是就在我們身邊,與日常生活的推論密不可分。
因此,我要鄭重推薦本書。這是一部極成功的普及書寫作品(作者想必投注相當的心力),值得我們普及作家仿效,更值得教師引入教育現場,充當閱讀良伴。」
推薦文
很難明白這其實很簡單
洪萬生 ( 台灣數學史學會理事長 )
本書作者喬丹.艾倫伯格在他的前一本普及書籍中,深入淺出地說明「數學教你不犯錯」,現在他的科普對象擴大成無所不在的「幾何學」,譬如「流行病傳播的幾何學、美國混亂政治過程的幾何學、職業棋士的幾何學、人工智慧的幾何學、英語的幾何學、財金的幾何學、物理的幾何學、甚至詩的幾何學」。儘管這些都是資訊、生物、策略、民主和所有事物背後隱藏的材料,就其繽紛多元的表面現象來看,的確有令人難以下手之處。然而,艾倫伯格在本書的論述與敘事,卻足以印證他對於「機器學習」vs.「人類學習」的(「先天」)強烈對比所給出的評論:「很難明白這其實很簡單」。當然,這句話是針對機器學習而發。
以著名的奇偶問題—也就是判斷X與O組成的字串中X的數量是奇數還是偶數為例,「標準的神經網路建構都把這題目學得很糟」。還有,如將機器學習應用在目前極夯的自駕車上,那也讓我們不無憂心。艾倫伯格的評論值得引述如下:「自駕車也許有95%的機率能做出正確選擇,但這不代表它在往永遠做出正確選擇的路上已走了95%;剩下的5%,也就是那些異常情況,也許正是人類散漫的大腦,比任何當前或近期可能出現的機器,更善於解決的問題。」
或許散漫的大腦更有品味,至於專擅演算法的機器則是完全「不解風情」。這應該也部分解釋了何以本書所引述的西洋棋冠軍拒絕與機器下棋。這是因為儘管「樹形幾何告訴你如何能贏;但不能告訴你是什麼讓一場遊戲變得美麗。那是更奧妙的幾何學,目前還不是電腦能依靠短短幾條規則一步步推出來的」。
當然,奉機器學習為圭臬者可能懷疑莫非艾倫伯格這個數學書呆子之淺見。不過,他就學哈佛大學期間,師承名師馬祖爾(Barry Mazur)主修代數數論,但是卻在研一下學期,選修了從魔術師變成哈佛數學系教授的戴康尼斯(Persi Diaconis)之「洗牌幾何」課程,可見他並非不食「人間煙火」。事實上,在本書第十四章,我們看到他發現「數學如何破壞民主(又如何加以挽救)」,其中更值得注意的,是他對於民主(或反民主)運作的投入瞭解,試圖運用很簡單的數學,解剖政黨競爭的爾虞我詐(他教職所在的威斯康辛州恰好就是「惡名昭彰」的搖擺州)。另一方面,在本書中,他也使用了許多篇幅,說明諾貝爾獎得主羅斯醫生如何利用隨機漫步過程來模擬蚊子的飛行,從而類比到疫病的傳播時間與路徑。「只要蚊子的密度夠低,魔法數字R0就會降到1以下,也就代表病例數會一週比一週少,疫情也會呈指數衰減。
你不必防止所有的傳播;只要防止足夠的傳播就行了。」因此,針對目前還正在肆虐全球的 COVID-19,他的建議與許多專家的看法一致:「我們不需要追求零擴散,雖然這樣當然很好,但不太可能。流行病的控制並不追求完美主義。」
最後,回到本文的主題。我想數學普及作家向讀者介紹很多高度抽象數學甚至只是一般數學知識時,也經常「很難 ( 讓人 ) 明白這其實很簡單」。這個難度涉及作家的數學洞識,有時還需輔以數學史洞識,至於敘事素養則更是不可或缺。本書作者學養博雅,又常能在卑之無甚高論的大眾問題日常中,發現極有意義的數學問題(譬如氣球戳破後有幾個洞?),再加上他擁有創意寫作的專業訓練,同時又十分關注數教育改革議題,因此他在書中總能適時地分享極有價值的點滴心得。譬如,論及海龍公式(本書譯成希羅公式)時強調:「長度的守恆暗示了三角形面積的守恆,因為兩個三角形如果邊長相等,就意謂著這兩個三角形全等,因此有同樣的面積;或者你可以運用亞力山卓的希羅那道優美古老的公式,那告訴你如何以邊長表示面積。」類似這樣的觀察,當然也可充實中學數學及通識教學內容。
再有,本書有關美國選舉制度及疫病(特別是 COVID-19)的數學問題(本書歸類為「幾何學」)之說明,一定可以讓關注或參與類似活動的博雅君子「感同身受」。中學教師也可以在課堂上引進這些例子及其說明,來強調數學並非遠在天邊的彩虹,而是就在我們身邊,與日常生活的推論密不可分。
因此,我要鄭重推薦本書。這是一部極成功的普及書寫作品(作者想必投注相當的心力),值得我們普及作家仿效,更值得教師引入教育現場,充當閱讀良伴。最後,我要引述作者對〈美國獨立宣言〉的備註,作為我這篇「掛一漏萬」的推薦文之結語:
「我們認為下面這些真理是不證自明的」不是傑佛遜的話;他的獨立宣言第一版草稿寫的是「我們認為下面這些真理是神聖而無可否認的」。
是富蘭克林刪去幾個字後換成「不證自明」,使得這份宣言少了些聖經味,多了點歐幾里得味。富蘭克林刪得好!「神聖而無可否認」vs.「不證自明」當然有著強烈對比,然而,「細節」之於風雅,或許就是本書作者關注之所在。
內文試閱
第二章
一根吸管有幾個洞?
對於我們這些專職於數學的人來說,每當網路上因為某個數學問題而糾結個一兩天,我們總是感到很開心,我們得以看著大家發現並享受我們一輩子樂在其中的思考模式。要是你有一棟很棒的房子,你會很樂見客人突然來訪。
通常能引起這類關注的問題都相當不錯,雖然一開始看似無聊,但能抓住眾人注意力的是遇到真正數學題目的那種感覺。
舉例來說:一根吸管有幾個洞?
大部分我問過的人都認為答案很明顯,當他們知道有人所謂OB的答案和他們的不同,他們通常會非常驚訝,甚至有點惱怒。這是數學版本的「還有別的想法等著你」(You’ve got another think coming)和「還有別的事等著你」(You’ve got another thing coming)之爭。
就我所知,吸管的洞這個問題,最早是出現在《澳大拉西亞哲學期刊》(Australasian Journal of Philosophy)1970年的一份論文,由夫妻檔史黛芬妮(Stephanie)和大衛路易斯(David Lewis)提出,當時討論的物體是紙巾捲筒。2014年這個問題以投票形式,再度出現在一個健身論壇裡。在健身論壇裡這個論述呈現的方式與《澳大拉西亞哲學期刊》不同,但爭議的重點很一致;「零個洞」、「一個洞」和「兩個洞」的回答各有大量支持者。
然後兩名大學朋友爭辨到底是一個洞還是兩個洞,結果愈來愈憤怒的SnapChat影片開始流傳開來,甚至吸引超過一百五十萬人次觀看。這個稻草問題開始傳遍Reddit和推特,還上了紐約時報。一群年輕、美麗帥氣、對洞極度困惑的BuzzFeed員工,拍攝了一支影片,同樣也獲得數十萬人次點閱。
也許你已經開始在心裡設想主要論述了,讓我們重述一遍:
零個洞:吸管是以長方形塑膠片捲起黏合而成,長方形沒有任何洞,你在將它捲起時也沒有打上任何洞,所以它還是沒有洞。
一個洞:這個洞就是吸管的中空部分,一直從頭延伸到尾。
兩個洞:看就知道了啊!上端一個洞,下端一個洞!
我的第一個目標是要說服你,你對有幾個洞感到困惑,即使你以為你沒有。這幾個看法都有嚴重瑕疵。
我先推翻零個洞的說法,一個東西不需被移去任何物質也可以出現洞。貝果的做法不是先做出實心麵包再打個洞,不是——你是揉出長條狀麵團,然後將兩端接合做成貝果。要是你否認貝果上有洞,你會被笑到在紐約市待不下去,或蒙特婁,或全世界任何有自尊的熟食店。我想不用多說了。
那兩個洞的論點呢?這裡有個問題值得想一想:要是吸管有兩個洞,一個洞結束而另一個洞開始的地方在哪裡?若你還不為所動,那就拿一片瑞士乳酪來說好了,有人要求你數它有多少洞,你是分別數上面有幾個洞和下面有幾個洞嗎?
或者這樣:把吸管的底端封住,這樣聲稱有兩個洞的人士所謂底部的洞就沒了。現在這吸管有點像是高高瘦瘦的杯子,杯子有洞嗎?有啊,你說——頂端的開口就是洞。好,那要是杯子變得愈來愈矮胖,直到變成煙灰缸呢?我們肯定不會說煙灰缸上面那一圈是「洞」吧?但要是在杯子變煙灰缸的過程中,洞消失了,那到底是何時呢?
你也許會說,煙灰缸還是有洞,因為它有個凹陷,一個本來可以有東西實際上卻沒有的負空間。洞又不是一定要「從頭通到尾」,你堅持——想想我們說地上有個洞是什麼意思!這是相當好的駁斥,但要是我們對什麼算洞的標準如此寬鬆,任何凹痕或缺口都算,那這個概念就會被擴大到毫無用處了。當你說水桶有洞,你的意思不是桶底有個凹痕,你是指它盛不住水。你在實心麵包上咬一口,也不會讓它變成貝果。
那就只剩下「一個洞」了,這也是三個選項中最多人選的。現在就讓我替你毀了它吧。當我問我的朋友凱莉(Kellie)關於吸管的問題時,她對一個洞理論的反駁非常簡單:「這代表嘴巴和肛門是同一個洞嗎?」(凱莉是瑜珈老師,所以會傾向以生理結構角度看事情),好問題。
但假設你是那些願意大膽接受「嘴巴=肛門」等式的人,還是有其他問題。在那對大學生的SnapChat影片裡有個場景(說真的,自己去看吧,我實在無法用文字和舞台指令,漂亮地傳達出那種逐漸累積的挫敗感),哥一是一個洞理論的代言人,哥二屬於兩個洞派:
哥二[拿起花瓶]:「這有幾個洞?這是一個洞,對吧?」
[哥一發出反對聲]
哥二[拿起紙巾捲筒]:「所以這有幾個洞?」
哥一:一個
哥二:「怎麼會?」[再度拿起花瓶]「這兩個有一樣嗎?」
哥一:「因為要是我在這裡打一個洞」[手指花瓶底] 「它還是一個洞啊!」
哥二[惱怒]:「你剛說,要是我在這裡打一個洞。」
[發出挫敗激動的聲音]
哥一:「要是我在這裡打一個洞那就是——」
哥二:「對——另一個洞,包括這個洞!兩個!結束!」
在這一幕中,兩洞派哥表達了一個令人激賞的原則:在一個東西上多加一個洞,理應增加它的洞數。
讓我們弄得更難一點:一件褲子有幾個洞?大多數人會說三個:腰部和腿的兩個洞。但要是你把腰部縫起來,就變成一個彎折的牛仔布大吸管。要是你一開始說有三個洞,那封上一個,應該剩下兩個洞,而不是一個——對吧?
若你是認為吸管只有一個洞,那也許你會說褲子只有兩個洞,那把腰部封住後就只剩一個。這個答案我經常聽到,但這個答案跟吸管兩洞理論有一樣的問題:要是褲子有兩個洞,是哪兩個,一個結束而另一個開始的地方又在哪裡?
或者你的看法是褲子只有一個洞,因為你所謂的洞,指的是褲子內部的負空間。那要是我在膝蓋的地方割一個洞呢?那也不算嗎?不算,你堅持,還是只有一個洞;你那巧妙地一割,只是讓洞多了一個開口。要是你把褲腳都縫起來,或是塞住吸管的底部,你也不是消除了洞,只是封住了洞的入口或出口。
但這又讓我們繞回到煙灰缸是否有洞的問題,或者更糟:假設我有一個吹大的氣球,根據你的說法,氣球有一個洞——也就是壓縮的空氣存在氣球內的區域。要是我拿針在氣球上刺一個洞,它會爆開,剩下的就是一個橡膠圓盤,也許上面還綁著一個結。一片圓形橡膠顯然沒有洞,所以你把本來有個洞的東西,刺了一個洞,然後它就沒有洞了。
你現在被弄糊塗了嗎?我希望如此!
數學沒有回答這個問題,並不完全。它無法告訴你,你說的洞(hole)這個字到底是什麼意思——那是你和與你對話者之間的問題。但它可以告訴你,你可能是什麼意思,那至少不會讓你被自己的假設絆倒。
先讓我從一個令人惱人的哲學口號開始,吸管有兩個洞;但它們是同一個洞。
……
第十章
今天發生的事明天也會發生
不太令人放心
羅斯關於流行病增長的看法,是受一潛在原則所主導,事實上它是所有數學預測暗含的那一個原則,也就是:今天發生的事,明天也會發生。所有勞神費力的細節,都是為了找出在實際運用時這代表了什麼。
這裡有一個最簡單的範例。假設一傳染性病毒帶原者,在感染期間平均感染另外兩人,而染病期間就說是十天好了。如果一開始有一千人感染,十天後就約有另外兩千人被感染。原來的一千人康復後不再感染,但下週這兩千人又會再感染另外四千人,再下一週又是另外八千人會染病。所以過了四週後的染病人數會是:
第 0 天:1000
第 10 天:2000
第 20 天:4000
第 30 天:8000
這種數列被稱為幾何級數(geometric progression),雖然它跟幾何的關聯有點隱晦。來源是這樣的:每個數字都是它前一數字及後一數字的幾何平均數(geometric mean)。可是平均數是什麼意思?幾何平均數又是什麼?
這裡的平均數也是一種平均值。你習慣的平均值應該是取在數線上兩個數之間的中點。例如1和9的平均值是5,因為5跟1差4,也跟9差4。這種叫做算術平均數(arithmetic mean),我想是因為它是從加減運算得出才有此命名。如果一個數列中的每個數都是它前一個和後一個數的算術平術數,這種數列就叫算術級數。
幾何平均數是另一種平均值,要取得1和9的幾何平均數,你要先畫出邊長為1和9的長方形。
幾何平均數是面積與此長方形相等的正方形的邊長(希臘人很愛用正方形來算面積;這是他們屢敗屢戰想要化圓為方的原因之一)。幾何平均數是柏拉圖的最愛,據說他認為幾何平均數是最真實的平均數。這個長方形的面積是1×9=9;如果一個正方形的面積與它相等,它的邊長就應該是自身相乘後等於 9 的數字,也就是以一種曲折冗長的方式來說3,所以1和9的幾何平均數就是3,而且1, 3, 9是一個幾何級數。
現在我們更習慣用一種不同但相等的方式來定義幾何平均數;數字x與z的幾何平均數為 y,則y/x=z/y。
與這條簡潔的公式相比,柏拉圖在鼓吹幾何平均數時,把自己繞進了多麼拗口的語言迷陣:
如今最好的聯結,是一種真真正正將自身與由它所聯結的事物結合在一起的聯結,而這在事物的本質上最好通過比例來實現。對任三個數而言,可以是實數或平方數,任何二數之間的中間項是這樣的,第一項之於它是什麼,它之於最後一項也是這樣;反過來說,最後一項之於中間項是什麼,它之於第一項也是這樣。因為中間項既是第一項又是最後一項,那麼最後一項和第一項同樣也都會是中間項,因此它們必然相互具有相同的關係,並且,有鑑於此,將全部結合為一。
現在知道代數符號的好了吧!
病毒以幾何級數擴散不是因為它們喜歡計算長方形面積,也不是因為它們讀過柏拉圖;它們這麼做是因為病毒擴散的機制,上週感染數與這週感染數的比率,會和這週感染數與下週感染數的比率相同。今天發生的事,明天也會發生,而在我們之前舉的例子中,每過十天,
新病例數就會乘以 2。當一個數列呈現增長的幾何級數時,我們說它呈指數式增長。人們常用「指數式增長」作為「飛速增長」的同義詞,但前者的定義明確許多。每位數學老師都很想要一個例子,能讓學生切身瞭解指數增長(exponential growth)如何表現。很不幸地,我們眼前
就有這樣一個例子。
人類原廠等級的直覺很難理解指數增長。我們習慣物體以等速前進,如果以時速 60 英里駕車,你每小時的行駛總距離會是
60英里、120英里、180英里、240英里⋯⋯
這叫做算術級數—前一項和後一項的差始終不變,數字以等速成長。
幾何級數就不同了;我們的心智把它們解讀成原本緩慢穩定可控的成長,突然以駭人幅度陡然上升。但就幾何學來說,成長的速度從未改變,這週和上週一樣,只是惡化了兩倍。這場災難完全是可預測的,但我們不知為何就是覺得難以預料。聽聽約翰.艾希伯里(John Ashbery)的話,他可能是唯一提到過幾何級數的美國重要詩人,他在1966 年的詩作〈最快補救〉(Soonest Mended)
就像幾何級數友好的開始
不太令人放心⋯⋯
在COVID-19爆發初期受創最深的義大利,疫情在最初一個月就奪走一千條人命,接下來的一千名死亡案例卻在短短四天內發生。在2020年3月9日,疫情早已擴散至全球之際,一名美國官員卻極力淡化這項威脅,拿它與每年死於流感的數千名美國人相比:「目前有五百四十六例新冠病毒的確診案例,二十二例死亡,想一想!」一週後每天有二十二名美國人死於 COVID-19,再一週後是將近十倍。
不過幾何級數有好的也有壞的。假設帶原者把他們的小小朋友平均傳給0.8人而不是 2 人,那麼感染的幾何級數就會是這樣:
第 0 天: 1000
第 10 天: 800
第 20 天: 640
第 30 天: 512
接下來的四個數字更漂亮:
第 40 天: 410
第 50 天: 328
第 60 天: 262
第 70 天: 210
這是指數衰減(exponential decay),一個輕掠而過的流行病的數學特徵。
這個數字—幾何級數中每一項與前一項的比率—意義重大。一旦它大於 1,病毒就會快速傳播到可觀比例的人口之中,如果它小於1,疫病就會消退。在流行病學圈中,它被稱為R0。在1918年春季爆發的西班牙流感,據估算R0為1.5,2015年至2016年透過蚊子傳播的茲卡(Zika)病毒則是2左右。至於麻疹,以1960年代的迦納(Ghana)來算是14.5 !
R0小的流行病看起來會是這樣:
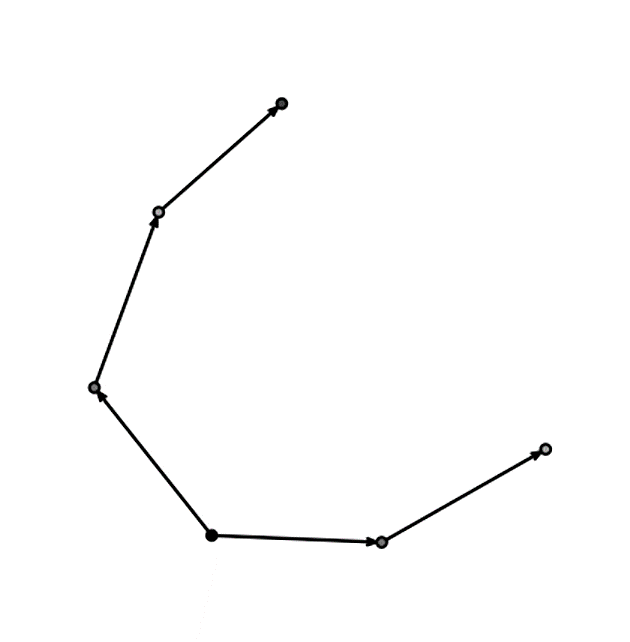
大多數人,如果有傳染給別人的話,只會傳染給一個人,感染鏈通常會漸漸消退,不會過度擴散。如果R0大於1,你就會看到它分枝出去:
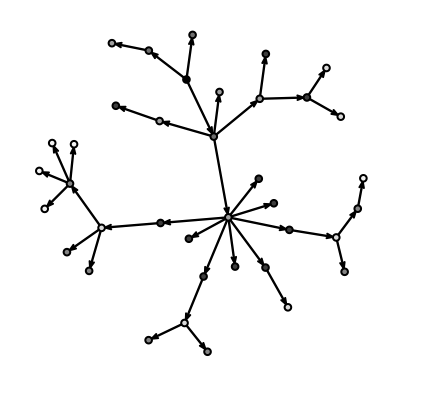
當R0比1大很多時,你就會看到快速的指數增長,疫情不斷分裂出新分枝,感染更多的人。
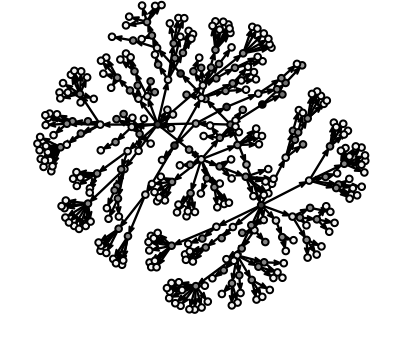
如果這種疾病在感染後就可免疫,這些分枝永遠不會回頭找上已經染病過的人,那麼這種疫病的網路就會像是我們之前看過的幾何圖形:樹形。
這個 R0=1 基本門檻的存在,是羅斯關於流行病的理論核心。羅斯發現瘧疾是透過蚊子傳播,這是一項重大進展,但這也造成某種程度的悲觀主義。要殺死蚊子很容易,但要殺死所有的蚊子就很難了。所以你可能會認為要阻止瘧疾擴散是不可能的任務。並非如此,羅斯堅持道。只要附近有瘧蚊,其中一些就會叮咬染上瘧疾的人,然後在附近亂飛,再叮咬還未染上瘧疾的人,所以瘧疾會不斷擴散。不過只要蚊子的密度夠低,魔法數字R0就會降到 1 以下,也就代表病例數會一週比一週少,疫情也會呈指數衰減。你不必防止所有的傳播;只要防止足夠的傳播就行了。
這正是 1904 年羅斯在聖路易博覽會上宣導的。他的隨機漫步論點則是為了說明,一旦某一地區的蚊子數量減少後,至少要花上一段時間,才會有足夠數量的蚊子遷回該區,以至於再度超過疫病門檻。這也是防治COVID-19的關鍵概念,我們不需追求零擴散,雖然這樣當然很好,但不太可能。流行病的控制並不追求完美主義。